
点击桌面的PyCharm图标,如图:

接着创建python文件。第一次使用PyCharm的界面如图所示:
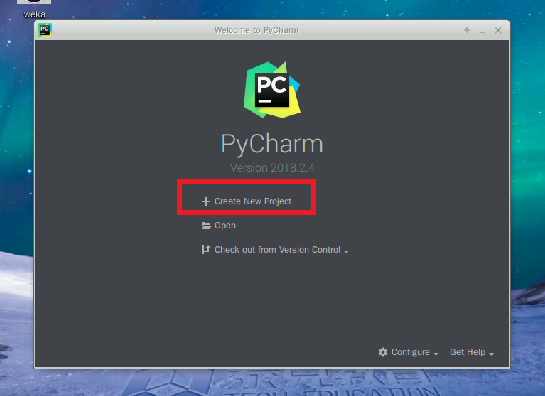
点击Create New Project创建项目,名字保持默认。进入下图界面:
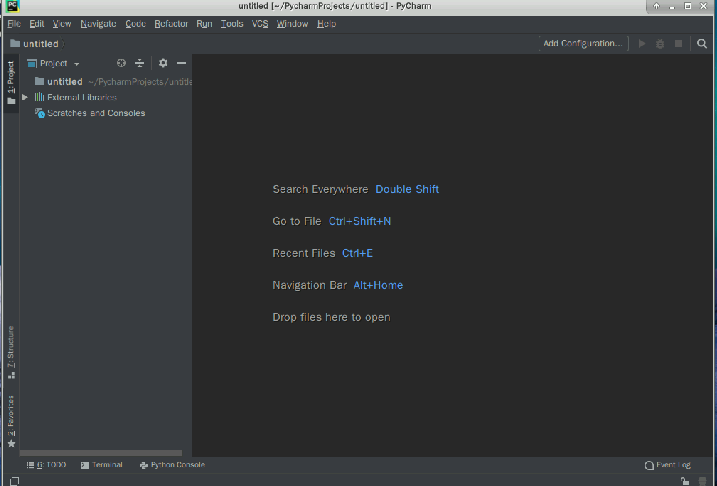
将鼠标移到untitled上,然后点击右键,会出现选择选择框,按照图中标志依次点击New->Python File。如图:
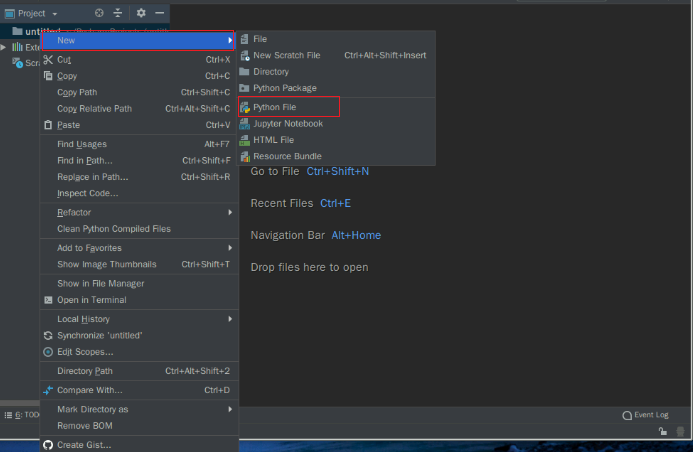
点击后弹出如下界面,Name栏中输入文件名,命名为LRegression,点击OK,就创建了一个.py程序。如图:
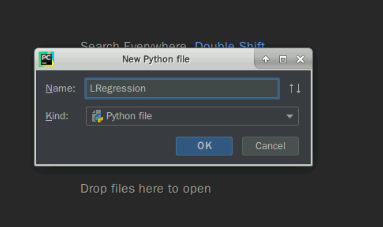
进入软件后,初始界面如下所示,左边为显示的当前文件夹和工作区,右边为命令行窗口,下方为输出窗口。
点击pycharm下方的Terminal
先安装“python3-tk”,输入如下命令,需要输入密码的时候,请输入Huawei@123
拷贝代码sudo apt-get install python3-tk
输入 pip install http://file.ictedu.com/fileserver/common/data/numpy-1.17.2-cp35-cp35m-manylinux1_x86_64.whl 安装numpy (注意:通常是pip install numpy,此处采用离线安装,后面也是)

输入以下命令安装matplotlib (注意:通常是pip install matplotlib)
拷贝代码pip install http://file.ictedu.com/fileserver/common/data/cycler-0.10.0-py2.py3-none-any.whl
pip install http://file.ictedu.com/fileserver/common/data/kiwisolver-1.1.0-cp35-cp35m-manylinux1_x86_64.whl
pip install http://file.ictedu.com/fileserver/common/data/python_dateutil-2.8.0-py2.py3-none-any.whl
pip install http://file.ictedu.com/fileserver/common/data/pyparsing-2.4.2-py2.py3-none-any.whl
pip install http://file.ictedu.com/fileserver/common/data/six-1.12.0-py2.py3-none-any.whl
pip install http://file.ictedu.com/fileserver/common/data/matplotlib-3.0.3-cp35-cp35m-manylinux1_x86_64.whl
首先通过在terminal中输入wget http://file.eduict.com/start/big_data_warehousemining/data/ex1data1.txt命令下载实验数据。 ex1data1中的数据表示城市移动餐车的利润和城市人口数量。 该程序的实现功能是:在已知某个固定城市人口数量时,预测移动餐车的利润是多少,以帮助用户选择在哪个城市进行新店扩张。 首先,导入相关的库以及python的编码方式:
拷贝代码wget http://file.ictedu.com/fileserver/big_data_warehousemining/data/ex1data1.txt

拷贝代码#!/usr/bin/python
# -*- coding: utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt
import numpy as np
import time
def loadData():
f = open('ex1data1.txt')
data = f.readlines()
l = len(data)
mat = zeros((l, 2))
index = 0
xdata = ones((l, 2))
ydata = []
for line in data:
line = line.strip()
linedata = line.split(',')
mat[index, :] = linedata[0:2]
index += 1
xdata[:, 1] = mat[:, 0]
ydata = mat[:, 1]
return xdata, ydata
def model(theta, x):
theta = np.array(theta)
return x.dot(theta)
def cost(theta, xdata, ydata, l):
SUM = 0
idex = 0
ydata = mat(ydata)
ydata = ydata.T
for line in ydata:
yp = model(theta, xdata[idex, :])
yp = yp - ydata[idex, :]
yp = yp ** 2
SUM = SUM + yp
idex = idex + 1
return SUM / 2 / l
def grad(theta, idex1, xdata, ydata, sigmal, l):
idex = 0
SUM = 0
for line in ydata:
yp = model(theta, xdata[idex, :]) - ydata[idex]
yp = yp * xdata[idex][idex1]
idex = idex + 1
SUM = SUM + yp
return SUM / l
def gradlient(theta, xdata, ydata, sigmal, l):
idex1 = 0
for line1 in theta:
theta[idex1] = theta[idex1] - sigmal * grad(theta, idex1, xdata, ydata, sigmal, l)
theta[idex1] = theta[idex1]
idex1 = idex1 + 1
return theta
def OLS(xdata, ydata):
start = time.process_time()
theta = [0, 0]
iters = 0
iters = int(iters)
l = len(ydata)
l = int(l)
cost_record = []
it = []
sigmal = 0.01
cost_val = cost(theta, xdata, ydata, l)
cost_record.append(cost_val)
it.append(iters)
while iters < 1500:
theta = gradlient(theta, xdata, ydata, sigmal, l)
cost_updata = cost(theta, xdata, ydata, l)
iters = iters + 1
cost_val = cost_updata
cost_record.append(cost_val)
it.append(iters)
end = time.process_time()
return mat(theta).T, cost_record, it
def show(xArr, yArr):
plt.xlabel('Population', size=25)
plt.ylabel('Profit', size=25)
plt.title('Linear Regression', size=30)
xCopy = xArr.copy()
xCopy.sort(0)
yHat = xCopy * ws
plt.plot(xArr[:, 1], yArr, 'go', label='y1')
plt.plot(xCopy[:, 1], yHat, label='y2')
plt.show()
def show1(xArr, yArr):
plt.xlabel('iters', size=25)
plt.ylabel('cost', size=25)
plt.title('Linear Regression', size=30)
plt.plot(xArr[0:, ], yArr[0:, ], 'go', label='y1')
plt.show()
xArr, yArr = loadData()
ws, cost_rec, iters = OLS(xArr, yArr)
test = [1, 3.5]
print("When the population is 35,000, the profit is:")
print(ws[0][0] * test[0] + ws[1][0] * test[1])
test1 = [1, 7]
print("When the population is 70,000, the profit is:")
print(ws[0][0] * test1[0] + ws[1][0] * test1[1])
show(xArr, yArr)
show1(mat(np.array(iters)), mat(np.array(cost_rec)))

首先按Ctrl+S保存,然后鼠标右键单击python文件,在弹出框点击“Run**”运行程序,如图:
如果没有错误,则会出现以下结果。 利润预测:
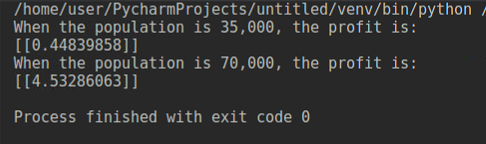
回归直线:
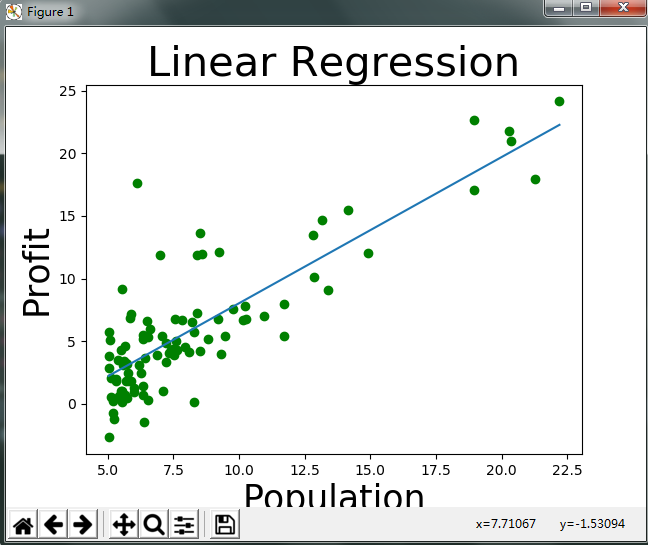
代价变化曲线: